DISTRIBUICIÓN
DE
FRECUENCIAS AGRUPADAS
Es aquella distribución en la que la disposición tabular de los datos estadísticos se encuentra ordenada en clases y con la frecuencia en cada clase; es decir, datos originales de varios valores adyacentes del conjunto se combinan para formar un intervalo de clase. No existen normas establecidas para determinar cuándo es apropiado utilizar datos agrupados o datos no agrupados; se sugiere cuando el número total de datos (N) es igual o superior de 50 y además el rango o recorrido de la serie de datos es mayor de 20, entonces se utilizará la distribución de frecuencias para datos agrupados, también se utilizara este tipo de distribución cuando se requiera elaborar gráficos lineales como el histograma, el polígono de frecuencia o la ojiva.
La razón fundamental para utilizar la distribución de frecuencias de clases es proporcionar mejor comunicación acerca del patrón establecido en los datos y facilitar la manipulación de los mismos. Los datos se agrupan en clases con el fin de sintetizar, resumir, considerar o hacer que la información obtenida de una investigación sea manejable con mayor facilidad
Al agrupar los datos en una distribución de frecuencias de clase s e pierde parte de la información. La reducción o agrupamiento a que son sometidos los datos de una serie de valores cuando existen muchos valores diferentes, originan los denominados errores de agrupamiento; cual la distribución de frecuencias de clases tiene una validez estadística práctica.
Clase o intervalo de clase. Son divisiones o categorías en las cuales se agrupan un conjunto de datos ordenados con características comunes. Para organizar los valores la serie de datos hay que determinar un número de clases que sea conveniente. En otras palabras, que ese número de intervalos no origine un número pequeño de clases ni muy grande. Un número de clases pequeño puede ocultar la naturaleza natural de los datos y un número muy alto puede provocar demasiados detalles como para observar alguna información de gran utilidad en la investigación. A las fronteras del intervalo,
En particular, a muchas personas les parece que el arte y la matemática son dos extremos expuestos, cuando en realidad pueden ser relacionados perfectamente.
Como ejemplo moderno se puede mencionar que la matemática y la música suelen ser imaginadas como disciplinas muy diferentes. Sin embargo es posible establecer un vínculo entre ambas tendencias. Ya hacia la época de Pitágoras, las enseñanzas contenían la aritmética y la música en conjunto. Nace la idea de la relación entre impares de sonidos, que se caracteriza mediante el cociente entre sus frecuencias. Los instrumentos musicales son capaces de producir lo que se llama una onda de presión, un empujón de aire que es capaz de mover pequeña membrana del oído que denominamos tímpano la frecuencia de vibración define lo que se conoce como nota.
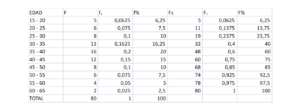
Si intentamos listar una en una tabla de frecuencias los 80 datos nos encontraríamos con una gran variedad e valores. Además, sus correspondientes frecuencias son similares. Ante este panorama el sentido común aconseja organizar los datos por edad.
Para poder usar, mas adelante con modalidad este material llamamos a esas franjas intervalos de clase y los describimos agregando para el conteo.
Graficar:
DIAGRAMA DE FRECUENCIAS 1
CONCLUSION.- Las conclusiones obtenidas en este punto pueden servir para tomar decisiones o hacer predicciones. El estudio puede comenzar de nuevo a partir de este momento, en un proceso cíclico que permite conocer cada vez mejor la cantidad de personas y edades de la empresa. El concepto de cantidad de personas v más allá de lo que comúnmente se conoce como tal, se precisa como conjunto finito de personas objetos que presentan características comunes.
El tamaño que tiene la cantidad de personas es un factor de suma importancia estos son muchos el proceso de o investigación y este tamaño vienen dado por el número de elementos que constituyen, según el número de elementos que constituyen. Cuando la cantidad de personas es muy grande es obvio que la investigación de todos los elementos se dificulte en cuanto al trabajo tiempo y costos necesarios para hacerlo. Es a menudo imposible o poco práctico pasar la totalidad de los individuos sobre si estos son muchos.
TRABAJO
DE
MATEMÁTICA II
Nombre.- Callapa Hilary Samuel
Institución.- “IEA”
Docente.- Alberto Vicente Palladino