REGRESION Y CORRELACION LINEAL.
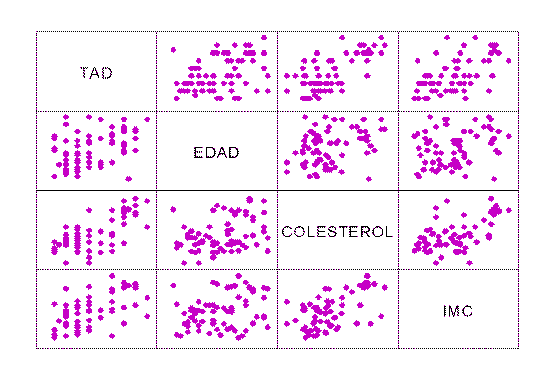
En esta nota pretendemos describir de manera clara y sencilla dos técnicas estadísticas de gran importancia – análisis de regresión y de correlación lineal.
Regresión lineal.
El análisis de correlación se encuentra estrechamente vinculado con el análisis de regresión y ambos pueden ser considerados de hecho como dos aspectos de un mismo problema.
La correlación entre dos variables es – otra vez puesto en los términos más simples – el grado de asociación entre las mismas. Este es expresado por un único valor llamado coeficiente de correlación (r), el cual puede tener valores que ocilan entre -1 y +1. Cuando “r” es negativo, ello significa que una variable (ya sea “x” o “y”) tiende a decrecer cuando la otra aumenta (se trata entonces de una “correlación negativa”, correspondiente a un valor negativo de “b” en el análisis de regresión). Cuando “r” es positivo, en cambio, esto significa que una variable se incrementa al hacerse mayor la otra (lo cual corresponde a un valor positivo de “b” en el análisis de regresión).
CORRELACION:
La correlación indica la fuerza y la dirección de una relación lineal y proporcionalidad entre dos variables estadísticas. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valoreshomónimos de la otra: si tenemos dos variables (A y B) existe correlación si al aumentar los valores de A lo hacen también los de B y viceversa. La correlación entre dos variables no implica, por sí misma, ninguna relación de causalidad.
RELACION ENTRE DOS VARIABLES:
Se dice que dos variables X e Y están relacionadas estadísticamente cuando conocida la primera se puede estimar aproximadamente el valorde la segunda, ejemplos:
Ingresos y gastos de una familia.
Mide el grado de relación lineal entre dos variables que varían conjuntamente.Pongamos un ejemplo, Supongamos que el Gerente de Personal de una empresa de servicios, cree que quizá haya relación entre el ausentismo y la edad; quiere tomar como punto de referencia a 5 trabajadores de distintas edades para desarrollar un modelo de predicción de días de ausencia, a continuación, los siguientes datos recolectados:
| Días | Edad (X) | Ausentismo (Y) |
| Lunes | 19 | 22% |
| Martes | 25 | 17% |
| Miércoles | 32 | 15% |
| Jueves | 42 | 12% |
| Viernes | 47 | 34% |
| 165/5 | 100/5 | |
| Mx=33 | My= 20 |
VAMOS A CALCULAR LOS SIGUIENES DATOS
- Calcular el coeficiente de correlación lineal
- La ecuación de regresión lineal
| (X-Mx) | (Y-My) | (X-Mx). (Y-My) |
| 19 -33 = -14 | 22 – 100 = -78 | -14. (-78) = 1092 |
| 25– 33 = -8 | 17 – 100 = -83 | -8. (-83) = 664 |
| 32 – 33 = -1 | 15 – 100 = -85 | -1. (-85) = 85 |
| 42 – 33 = 9 | 12 – 100 = -88 | 9. (-88) = -765 |
| 47 – 33 = 14 | 34 – 100 = -66 | 14. (-66) = -924 |
| Total = 152 |
| (X– Mx)2 | (Y – My)2 |
| -14. (-14) = 196 | -78. (-78) =6084 |
| -8. (-8) = 64 | -83. (83) =6889 |
| -1. (-1) = 1 | -85. (-85) =7225 |
| 9.9= 81 | -88. (-88) =7744 |
| 14.14= 196 | -66. (-66) =4356 |
| Total = 538 /5 | Total =32298 /5 |
| = 107,6 ?107,6 varianza | = 6459,6 ?6459,4 varianza |
| ?x = 10,37 | ?y = 80,37 |
Podemos decir que
R =1/5+152:(10,3*80,3)
R= 1/5 * 152/833,43
R = 152/4167,15
R = 0,0364 %
Ecuación Lineal
Y – My = R. . (X- Mx)
Y -20 = 0,0364 * *33
Y-20= 0,0364*7,750*33
Y= 9,3093 +20
Y=29,3093