Programación lineal
Una panadería desea maximizar la utilidad de sus dos productos más vendidos que son las medialunas de grasa y las medialunas de manteca. Para producirlas se necesitan dos maquinas: A y B. La información del tiempo de producción para cada máquina se encuentra en la siguiente tabla:
| Maquina A | Maquina B | |
| Medialunas de grasa | 1 hora | 2 horas |
| Medialunas de manteca | 3 horas | 2 horas |
Las horas que los empleados tienen disponible por día para producir son: para operar con la maquina A 24 horas y para operar con la maquina B 24 horas. Si las utilidades de cada medialuna de grasa y manteca son $20 y $25, respectivamente. ¿Cuántas medialunas de cada una deben producir por día para maximizar la producción? ¿Cuál es la utilidad máxima?
- Incógnitas
- Medialunas de grasa = X
- Medialunas de manteca = Y
- Función objetivo
F(x) = 20X + 25Y
- Restricciones
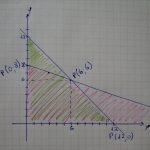
X + 3Y < = 24
2X + 2Y < = 24
X + 3Y= 24 2X + 2Y= 24
3Y= 24 – X 2Y= 24 – 2X
Y= 8 – 1/3X Y= 12 – X
8 – 1/3X = 12 – X Y = 12 – 6
-1/3X + X = 12 – 8 Y = 6
2/3X = 4
X = 4 . 3/2
X = 6
0 = 12 – X
X = 12
Función objetivo
F(0;8) = 20 . 0 + 25 . 8= 200
F(6;6) = 20 . 6 + 25 . 6= 270
F(12;0) = 20 . 12 + 25 . 0= 240
Para maximizar la producción debe producir 6 medialunas de grasa y 6 medialunas de manteca. Su utilidad máxima es de $270.