TRABAJO PRÁCTICO FÍSICA 1
Profesor de la asignatura: Damian Moscovitz
Nombre del Alumno: Lucas Dario Iratzabal
Curso Seguridad e Higiene: Primer año – Turno Mañana
Año 2018

Magnitud Física
Es una propiedad medible de un sistema físico, es decir, a la que se le pueden asignar distintos valores como resultado de una medición o una relación de medidas. Las magnitudes físicas se miden usando un patrón que tenga bien definida esa magnitud, y tomando como unidad la cantidad de esa propiedad que posea el objeto patrón.
Por ejemplo, se considera que el patrón principal de longitud es el metro en el sistema internacional de unidades.
Existen magnitudes básicas y derivadas, que constituyen ejemplos de magnitudes físicas: la masa, la longitud, el tiempo, la densidad, la temperatura, la velocidad y la aceleración.
En términos generales, es toda propiedad de los cuerpos que puede ser medida. De lo dicho se desprende la importancia fundamental del instrumento de medición en la definición de la magnitud.
Tipos de Magnitudes Físicas
Según su expresión matemática, las magnitudes se clasifican en escalares, vectoriales.
- Las magnitudes escalares son aquellas que quedan completamente definidas por un número y las unidades utilizadas para su medida. Esto es, las magnitudes escalares están representadas por el ente matemático más simple, por un número. Podemos decir que poseen un módulo pero carecen de dirección. Su valor puede ser independiente del observador (v.g.: la masa, la temperatura, la densidad)
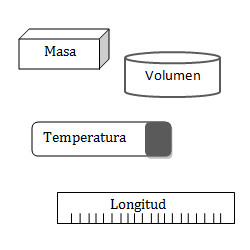
- Las magnitudes vectoriales son aquellas que quedan caracterizadas por una cantidad (intensidad o modulo), una dirección y un sentido. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa mediante un segmento orientado. Ejemplos de estas magnitudes son: la velocidad, la aceleración y la fuerza.

Vector Método analítico
- Existen dos formas de obtener la resultante por método analítico, el del triángulo y el de las componentes. Se presenta la descripción del método más utilizado que es el de las componentes.
- Se descomponen los vectores en sus componentes rectangulares.
- Las coordenadas del vector suma (resta) se calculan sumando las respectivas componentes de los vectores que se adicionan.
- El módulo del vector resultante se calcula con la ecuación:
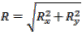
- La dirección y sentido se calcula por la fórmula trigonométrica:
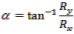
- Para aplicar el método del triángulo en la suma o resta de dos vectores, se analiza los elementos del triángulo formado por estos vectores y la resultante.
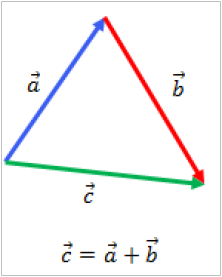
- Conociendo la longitud de dos lados (en este caso la longitud de los vectores y el ángulo entre ellos es posible calcular la longitud de la resultante por la ley de los cosenos:
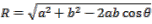
- El ángulo ? entre la resultante y el eje x (este ángulo determina la dirección y sentido de la resultante) se calcula por la ley de los senos:
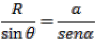
Método gráfico
Ese método es utilizado para la suma de exclusivamente dos vectores y consiste en la colocación de uno o continuación del otro.
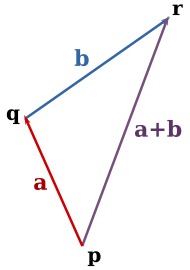
Pasos para realizar este método:
- Se traza un eje de coordenadas.
- Trazamos el primer vector poniendo el origen en el centro de nuestros ejes.
- En el extremo del primero vector trazamos un nuevo eje de coordenadas.
- Trazamos el segundo vector en el centro del nuevo eje.
- Se une al origen del vector 1 con el extremo del vector 2.
- Se mide la longitud y el ángulo de este nuevo vector, estos son nuestros resultados.






